Công thức tính thể tích hình trụ và bài tập có đáp án mới nhất 2023
Như các em đã biết, hình trụ tròn là hình có hai mặt đáy là các hình tròn song song và bằng nhau, có thể gồm một số vật thể hình trụ như lon sữa bò, cốc, chậu hoa, v.v. thùng, xô,… Cách tính thể tích của khối trụ cũng khá đơn giản và có nhiều ứng dụng trong thực tế, hãy cùng xem công thức tính thể tích của khối trụ như thế nào nhé.
Xem thêm : Bằng Tốt Nghiệp Đại Học | Không Bằng Đại Học Làm Phiên Dịch Viên Được Không? | Các khối học cấp 3 hiện nay gồm những khối nào? | Thủ tục chuyển trường đại học năm 2023
Cách tính thể tích khối trụ tròn và bài tập ví dụ
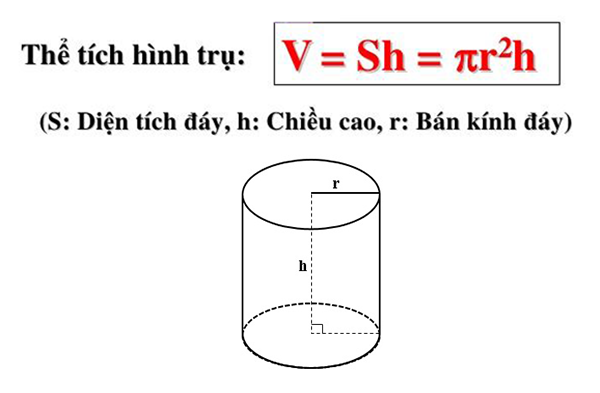
I. Công thức tính thể tích hình trụ
– Để tính thể tích của khối trụ tròn ta áp dụng công thức sau: V = π. r2. h
Với:
V là ký hiệu âm lượng
r là bán kính đường tròn đáy của hình trụ
h là chiều cao của hình trụ
là một hằng số ( = 3, 14)
– Đơn vị thể tích: mét khối (m3)
– Phát biểu bằng lời: Muốn tính thể tích của hình trụ ta nhân chiều cao với bình phương bán kính đáy hình tròn và số pi.
Ví dụ minh họa: Tính thể tích khối trụ biết bán kính hai đáy bằng 7,1 cm; chiều cao bằng 5 cm.
Hướng dẫn giải bài tập: Các em chỉ cần áp dụng công thức tính thể tích khối trụ, thay các số vào rồi tính. Ta có, thể tích khối trụ là: 3,14 x (7,1)2 x 5 = 791,437 (cm3)
Các em vận dụng công thức tính thể tích khối trụ trên để giải các bài tập tính thể tích khối trụ tròn, tính thể tích khối trụ ngoại tiếp hình lập phương cạnh a, tính thể tích khối trụ có bán kính đáy bằng a nội tiếp trong mặt cầu bán kính 2a,…
Cách tìm các đại lượng trong bài toán tính thể tích khối trụ
1. Tìm bán kính cơ sở
– Ban có thể tính bất kỳ diện tích đáy nào vì cả hai đáy đều bằng nhau. – Nếu không biết số đo bán kính đáy, bạn dùng thước đo khoảng cách rộng nhất trên hình tròn rồi chia kết quả đó cho 2 vì r = 1/2.d (d là ký hiệu của đường kính). Ví dụ: Em đo được khoảng cách là 5 cm, để tìm bán kính r em lấy 5 : 2 = 2,5 (cm)
*Chú ý: Đường kính là dây cung dài nhất của hình tròn nên khi đo đường kính em chọn cạnh của hình tròn trùng với gốc 0 của thước rồi đo chiều dài lớn nhất mà không làm động tác đó. Tham chiếu gốc di chuyển để tìm độ dài của đường kính.
2. Tìm diện tích đáy của hình tròn
– Để tìm diện tích đáy hình tròn ta áp dụng công thức tính diện tích hình tròn: A = π.r2 trong đó A là kí hiệu diện tích đáy hình tròn, r là bán kính hình tròn (đáy của hình trụ). Ví dụ: Tính diện tích hình tròn có r = 6,5 cm. => Diện tích hình tròn đáy là: 3,14 x (6,5)2 = 132,665 (cm2)
3. Tìm chiều cao của hình trụ
– Định nghĩa chiều cao của hình trụ: Là khoảng cách của 2 đáy ở mặt bên. – Nếu không biết chiều cao của hình trụ, có thể lấy thước đo chính xác độ dài của chiều cao, sau đó thế vào công thức tính thể tích hình trụ. Công thức tính thể tích khối trụ và áp dụng vào giải bài tập tìm đại lượng biết thể tích khối lăng trụ cũng khá đơn giản dễ hiểu, dễ nhớ nên học sinh dễ dàng ghi nhớ và vận dụng vào cuộc sống hàng ngày. các vấn đề. Ngoài ra, các em cũng nên tham khảo thêm bài tập nâng cao tính thể tích hình trụ ngoại tiếp cạnh hình lập phương và các bài viết chia sẻ công thức tính diện tích hình trụ được chia sẻ trên Taimienphi.vn để nắm được đầy đủ. Toàn bộ phạm vi bài viết về xi lanh. Nếu bạn có cách giải toán hay, hãy chia sẻ với chúng tôi để việc giải toán trở nên nhanh chóng và dễ dàng hơn. Tôi hy vọng bạn luôn yêu thích toán học nói chung và hình học nói riêng.
III. Bài giải ví dụ về diện tích và thể tích hình trụ trong SGK
- Giải bài tập 6 Toán 9 tập 2 trang 111
Chiều cao của hình trụ bằng bán kính của hình tròn đáy. Chu vi hình trụ là 314 cm2. Tính bán kính đường tròn đáy và thể tích của hình trụ (làm tròn đến hai chữ số thập phân).
hướng dẫn giải
Diện tích xung quanh hình trụ là 314cm2
2.π.r.h = 314
Rằng r = h
Vậy 2πr2 = 314
⇒ r2 50
⇒ r ≈ 7,07 (cm)
vậy thể tích của hình trụ là: V = π.r2.h = π.r3 ≈ 1109,65 (cm3). 2. Giải bài tập SGK Toán 9 Tập 2 trang 112
Hãy tính:
a) Tính chu vi hình trụ có chu vi đáy là 13 cm, chiều cao là 3 cm. b) Thể tích của hình trụ có bán kính đường tròn đáy là 5 mm và chiều cao là 8 mm.
hướng dẫn giải
a) Ta có: C = 13cm, h = 3cm
Chu vi của hình trụ là:
Sxq = 2πr.h = C.h = 13.3 = 39 (cm2)
b) Ta có: r = 5mm, h = 8mm
Thể tích của hình trụ là:
V = πr2.h = π. 52,8 = 200π 628 (mm3)
- Bài 11 trang 112 SGK Toán 9 Tập 2
Một bức tượng nhỏ bằng đá được ngâm hoàn toàn trong một bình thủy tinh hình trụ chứa đầy nước (h.84). Diện tích đáy lọ thủy tinh là 12,8 cm2. Nước trong bình dâng lên 8,5 mm. Khối lượng của bức tượng đá là bao nhiêu? hướng dẫn giải
Thể tích của tượng đá bằng thể tích của hình trụ có diện tích mặt đáy là 12,8cm2 và chiều cao 8,5mm = 0,85cm (Vì thể tích của tượng bằng thể tích của phần nước dâng lên). VÌ THẾ:
V = Sh.h = 12,8. 0,85 = 10,88 (cm3)
=> Xem thêm hướng dẫn giải bài tập trang 110, 111 SGK toán 9 tập 2 để hình dung cách làm, vận dụng công thức thể tích trong giải bài.
IV. Mọi người cũng hỏi
Công thức tính thể tích của hình trụ là gì?
Công thức tính thể tích của hình trụ là V = πr²h, trong đó V là thể tích, π (pi) là một hằng số gần bằng 3.14, r là bán kính đáy của hình trụ và h là chiều cao của hình trụ.
Tại sao công thức tính thể tích hình trụ dùng π (pi)?
Hình trụ có dạng giống với phần trên của một hình cầu, và π là tỷ lệ giữa chu vi đường tròn và đường kính của hình cầu. Vì vậy, π được sử dụng để tính thể tích hình trụ.
Công thức tính thể tích hình trụ áp dụng trong trường hợp nào?
Công thức này được áp dụng khi bạn muốn tính thể tích của một hình trụ có đáy là một đường tròn và có chiều cao. Đây là tình huống thường gặp khi tính thể tích của các hình trụ đứng, thùng chứa, và các cột trụ trong kiến trúc.
Có cách tính thể tích hình trụ khác ngoài công thức cơ bản không?
Ngoài công thức cơ bản, bạn cũng có thể sử dụng phương pháp tích phân để tính thể tích hình trụ trong các tình huống phức tạp hơn, như khi hình trụ có đáy không phải là đường tròn.
